Generalizando en Matemática

Generalizar, según la Real Academia Española, significa: “Abstraer lo que es común y esencial a muchas cosas, para formar un concepto general que las comprenda todas”. Excelente definición, suficientemente clara y con palabras fáciles y precisas, la cual se ajusta muy bien a todas las disciplinas, en especial a la Matemática.
En Matemática, la generalización está íntimamente relacionada con la abstracción y es que, a partir de la generalización, uno puede abstraer conceptos y propiedades. Nuestros alumnos, al llegar al secundario, ya han abstraído muchos conceptos y propiedades, quizás no de forma cociente, sino como algo natural. Así vemos que, para comprender el concepto de número o los algoritmos de las operaciones y sus propiedades, han tenido que abstraerlos y, por lo tanto, generalizarlos. El hecho de que, sepan que al ver el símbolo “2”, se están refiriendo al número que representa la cantidad conocida como dos, indica que ya en sus mentes se ha producido un proceso de generalización y abstracción.
Ahora bien, entrados en el secundario, debemos ya dar nombre y concientizar a los alumnos sobre este proceso de generalización y hacerlos protagonistas del mimo. Uno de los motivos de la importancia de esto, es que da un sentido previo a la enseñanza del planteo y resolución de ecuaciones, lo cual nos ayuda a familiarizar a los chicos con el lenguaje matemático y su equivalencia en el lenguaje coloquial.
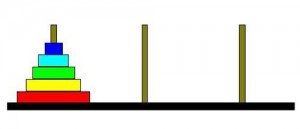
Existen muchas estrategias y diversidad de actividades para introducir, ejercitar y fortalecer la capacidad de generalización en nuestros alumnos. Una de las estrategias, que sirve y es interesante, pero sobre todo divertida, para introducir a los chicos en este proceso, consiste en estimular su sentido de generalización a partir de provocar y despertar su curiosidad. El recurso que les voy a presentar es un recurso lúdico conocido como “Torre de Hanói”.

Torre de Hanói

• Elementos necesarios: cartulinas de 3 o 4 colores distintos, compás y tijera.
• Consignas para armar el juego:
1. Dibujar con el compás círculos de distintos radios sobre las cartulinas (dependiendo de la cantidad de círculos con los que se quiera trabajar, yo recomendaría utilizar como máximo 6 círculos y construirlos con las siguientes medidas: uno de 6 cm de radio, otro de 5cm, de 4cm, de 3cm, de 2 cm y de 1 cm) teniendo en cuenta que, dos círculos de medidas consecutivas, deben ser de distinto color. Recortarlos con una tijera; a cada uno de ellos los llamaremos “discos”
2. Sobre un pedazo de cartulina o en una hoja, dibujar tres círculos de 10cm de radio, uno al lado del otro de forma horizontal y a la misma altura. Remarcarlos con un fibrón o fibra.
• Reglas del juego: apilamos los discos sobre uno de los círculos dibujados, empezando por el disco más grande hasta el de menor radio, de modo que, al ser de distintos colores, se deberían diferenciar todos uno encima del otro. El juego consiste en pasar todos los discos apilados en uno de los círculos, hacia alguno de los otros dos círculos vacantes. Para realizar este objetivo, es necesario seguir tres reglas:
1. Sólo se puede mover de a un disco a la vez.
2. Cada disco no puede colocarse encima de uno más pequeño que él mismo.
3. Sólo se puede desplazar el disco que se encuentre arriba de todo en cada pila.
Lo ideal es comenzar primero jugando sólo con dos discos, luego con tres y así sucesivamente, hasta llegar a jugar con los seis discos apilados.
• Consigna para despertar curiosidad: los alumnos deben tratar de realizar el pasaje de cada pila de un círculo a otro con la menor cantidad de pasos posibles. Luego se les dará la siguiente tabla para que completen con el dato pedido.

Cada vez que un alumno o grupo de alumnos encuentre la cantidad mínima de movimientos, se irá completando la tabla en el pizarrón, para que todos sepan que, menos que esa cantidad de movimientos, no pueden hacer y, para que todos se guíen de la misma sucesión de números para hallar, por último, una generalidad.
La idea es justamente que, luego de un tiempo de juego, ellos encuentren una regla general, es decir, que generalicen la cantidad de movimientos necesarios para ordenar n discos de un círculo a otro.
Así los chicos construyen su material, juegan, experimentan, ponen a prueba su ingenio y descubren su poder de generalización. Obviamente, luego de esta introducción, se debe institucionalizar la herramienta de generalización y seguir enriqueciéndola con nuevas y variadas actividades.
Por último y como recomendación para integrar a las nuevas tecnologías al trabajo matemático, en el caso de que en la escuela se cuente con una sala de computación, la construcción del material para el juego se puede obviar, ya que existen páginas donde se puede jugar a la Torre de Hanói online.
Dejo en el siguiente link una de estas páginas: http://www.disfrutalasmatematicas.com/juegos/torre-de-hanoi-2.html