
![]()
1 ¿Por qué y para qué aprender matemáticas?
Basta mirar a nuestro alrededor para encontrar respuesta a esta cuestión. Si queremos saber la hora miramos el reloj sea este el del móvil o el clásico (de pared o muñeca) o el que figura en la esquina de la pantalla de nuestro televisor. Cuando nos despertamos, ¿qué es lo primero que hacemos? ¿Cómo se construyó la casa donde vivimos? Y para adquirir nuestros alimentos cotidianos, ¿a dónde vamos? ¿Cómo llegan a nuestras manos? ¿Cómo se determina si nuestro organismo funciona bien? ¿Cómo se realizan los estudios clínicos y qué muestran sus informes? ¿Cuántas calorías son apropiadas para nuestra salud? Tantas cosas que para funcionar en nuestro mundo requieren de la matemática. Recuerdo a Emma Castelnuovo, uno de cuyos libros casi comienza con una reflexión: Un mundo sin números. ¿Cómo sería? Para bien o para mal, debemos el nuestro a, entre otras ciencias, la matemática. Con mayor o menor profundidad, con más o menos contenidos, nadie puede prescindir de esta materia y por ello ocupa, en todos los países, un lugar importante en los planes de estudio.
2. ¿Quiénes son para usted los matemáticos que a nivel mundial revolucionaron este conocimiento? ¿Por qué?
Los matemáticos, o sea aquellos que “inventan” la matemática, son personas que han dedicado su vida a resolver problemas. Los que diseñaron la matemática elemental nos son desconocidos, pertenecen a la noche de los tiempos y seguramente a la prehistoria, por lo que no los conocemos. Estoy convencida de que antes de crearse el lenguaje escrito, se crearon los primeros signos matemáticos, como marcas en la madera, en la roca o nudos en sogas, para contabilizar cantidades de individuos en un rebaño o en un grupo humano.
Creo que cuando sólo se sabía sumar y restar, fue un ignoto escriba que al resolver estas operaciones (por métodos muy tediosos y aburridos), observó sumas repetidas (o de sumandos iguales) una y otra vez. Y para evitar un nuevo
cálculo aburrido y tedioso, anotó de modo abreviado cada resultado y así fue creada la primera tabla de multiplicar.
Con el andar del desarrollo humano, los conocimientos se fueron acumulando a la vez que surgieron nuevos problemas para resolver. Y estos problemas se originaron en el entorno de la vida comunitaria(problemas extramatemáticos) o en el análisis de los mismos conocimientos matemáticos que llevaron a plantearse interrogantes al respecto (problemas intramatemáticos). Estos últimos se generan a partir de la propia curiosidad al reflexionarsobre resultados logrados.
Se sabe que el origen de la estadística se debe a una persona que realizaba tareas administrativas como las llamaríamos actualmente, en una “oficina” hospitalaria. Se “entretuvo” mirando los registros anuales de las dolencias por las que eran asistidos los pacientes y se dio cuenta de que ciertas enfermedades eran más frecuentes en determinadas épocas del año y decidió elevar un informe al rey respecto de estas observaciones. Así nació la stadística cuyo nombre deriva de estado, en el sentido de organización política. Esta situación aquí descripta se aproxima a un problema extramatemático. Pero también desde las otras áreas de la vida humana (no siempre relacionadas con la ciencia) surgen problemas para los que se necesita una respuesta matemática. A modo de ejemplo, sabemos que el Caballero de Meré se presentó ante Blas Pascal luego de haber perdido una fortuna en un juego de azar, para que le diera respuesta a la mejor manera de apostar en el mismo. Ese era su problema y Pascal creó la Teoría de las Probabilidades para encontrar la respuesta. No sé qué tiempo pudo haberle su elaboración pero la respuesta derivó en una nueva rama matemática.
Por supuesto que en el interior de la matemática surgen otras cuestiones que son las que reciben el nombre de intramatemáticas y cuya solución originan nuevos conocimientos matemáticos (dejo constancia de que algunas se logran encontrar o pronto o luego de varios siglos). Aunque dichos conocimientos parecieran no tener aplicaciones, estas están latentes o aparecen en las otras ciencias preguntas para las que casualmente ya los matemáticos dieron la
respuesta.
Si me pide un ejemplo simpático y accesible al público en general, muestro el siguiente:
Si se considera un número primo y a este se le suma la cantidad dos y se obtiene un nuevo número primo, se dice que tenemos una pareja de primos gemelos como en el caso de 5 y 7. Si en lugar de sumar dos sumamos cuatro, e tiene un par de primos primos, como el caso de 3 y 7. Si la diferencia entre dos números primos es seis, ellos se denominan primos sexys, como 7 y 13.
Sabemos que hay infinitos números primos, lo cual se demuestra sencillamente. La comunidad matemática se preguntó cuántas parejas de primos gemelos hay. Todavía no se encontró respuesta a esta cuestión, se conjetura que son infinitas pero en realidad no se sabe. En medio de la búsqueda de la solución, se ha producido mucha matemática.O sea, cualquier matemático crea matemática para resolver problemas y todos ellos logran revolucionar la matemática y tienen trascendencia universal.
3. En la vida diaria les puede decir a nuestros alumnos porque lasmatemáticas son importante para que se amiguen con esta materia escolar?
Es imposible que los estudiantes se amiguen con la matemática si no le encuentran significación (término este que se refiere al concepto) y sentido (procedimiento) a lo que hacen. Creo que casi cualquier niño encuentra significado a la suma y a la diferencia de números naturales. Esto es así porque generalmente, en su enseñanza, se parte de una situación problemática y se permite calcular con representaciones concretas de las cantidades (palitos,piedrecillas, porotos, dedos, etc.). Así, el aprendiz puede encontrar la cantidad que corresponde a la respuesta que la situación problemática solicita. En otras palabras: Si el docente comienza su clase por medio de una situación como “mi rosal tiene siete rosas y corto cuatro para poner en un florero, ¿cuántas rosas quedan en el rosal?” seguramente por medio de representaciones diversas (dibujos, uso de palitos, dedos …) los niños darán la respuesta. Nótese que no se pide en ningún momento que escriba la cuenta 7 – 4 = 3. Este será el resultado final del tiempo destinado a la enseñanza de la resta (que no es una clase ni una semana). Pero por lo general, las clases comienza con el anuncio docente de que se aprenderá a restar números naturales, ¿qué estudiante puede interesarse si para él no tiene ningún sentido la palabra “restar”? Sí tiene sentido un problema en un contexto adecuado porque es lo que da sentido al trabajo manual e intelectual que realiza el niño para resolverlo.
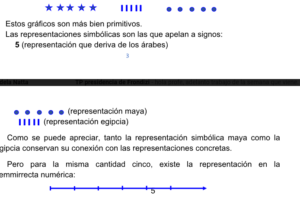
Manteniéndome siempre en ejemplos muy simples (estoy hablando con una colega en historia) se me ocurre reflexionar sobre la siguiente situación: Un número tiene distintas representaciones (es decir, diferentes formas de ser “escrito”). Por lo general hay (entre otras) representaciones gráficas y simbólicas. La cantidad cinco representación lingüística) puede asumir las siguientes representaciones gráficas:
Como se puede apreciar, tanto la representación simbólica maya como la egipcia conservan su conexión con las representaciones concretas.
Pero para la misma cantidad cinco, existe la representación en la semmirrecta numérica:
Cuando mi hermana tenía su niña en primer grado, me mostró esta representación en el cuaderno de mi sobrina y me preguntó con un gesto “¿y esto?”
Tenía razón. Para ella, persona adulta y con título universitario, la representación carecía completamente de sentido. ¡Qué decir de su hija! En estas circunstancias, ¿qué interés puede tener esa representación? La verdad, es que es muy útil en matemática, pero para un aprendiz escolar … Si Ud. me pregunta: “entonces, ¿no debería ser eliminado ese tipo de representación en primer grado?”, yo le respondería que hay que buscarle previamente un contexto adecuado que tenga sentido para el niño. Si ese contexto existe, debe estar en los contenidos de primer grado. En este momento se me ocurre que bastaría con preguntar el domicilio de una persona (de cualquiera de los niños). En un medio urbano, la respuesta sería una calle y un número. Y, ¿por qué es necesario un número? La respuesta es obvia: la calle es larga (sería modelizada por una semirrecta) y como hay muchas casas (puntos de la semirrecta) hay que tomar una decisión para encontrar el domicilio buscado. Fíjese que hay varias respuestas posibles: poner en el frente de cada casa el apellido de familia que allí vive, o una letra, o un número. Se optó por esta última alternativa, porque para encontrar la casa habría, probablemente, que caminar mucho y las letras se acaban demasiado rápido y los apellidos pueden coincidir.
¿Cuál es entonces la respuesta a su pregunta? Si las clases de matemática proponen a los estudiantes cada tema en una situación problemática con un contexto adecuado, no hay que justificar ante nadie por qué esta ciencia es importante en la vida diaria para que los alumnos se amiguen con ella.
Perfil de Estela Aliendro
Profesora de diversas asignaturas de Matemática en la Universidad Católica de
Salta, en la Universidad Nacional de Salta.
Profesora de Didáctica de la Matemática en la Universidad Nacional de Jujuy.
Profesora de Matemática en diferentes instituciones de nivel medio y terciario, de
gestión pública y privada en la ciudad de Salta.
Capacitadora de docentes. Vicedirectora del Colegio Secundario Nº 5047 “Dr. Benjamín Zorrilla”, Salta.
Responsable de la Cátedra de Matemática I en la Universidad Nacional de Salta.
Co-Directora del Proyecto de Investigación Nº 1467/0 del Consejo de Investigación
de la Universidad Nacional de Salta.
Directora y codirectora de tesinas de grado, de especialización y de tesis de maestría.
Autora y coautora de ponencias en Jornadas y Congresos de Educación Matemática en ámbitos nacionales e internacionales.
Autora y coautora de publicaciones en relación con la enseñanza de la Matemática.





Sé el primero en comentar