Breve Biografía:
El filósofo griego Tales, más conocido como “Tales de Mileto”, ya que nació en Mileto, una ciudad griega de Jonia (hoy Turquía) en el año 625 a.C. fue uno de los siete sabios de Grecia.
Es considerado el primer filósofo griego, por haber buscado una explicación racional de la realidad, alejada de los mitos, lo sobrenatural o lo religioso, basándose en que, si la realidad es física, su explicación también lo es. Toma como arjé, es decir, como principio u origen de todas las cosas, el agua. Todo lo que vive está constituido por agua, afirmaba que la tierra donde vivimos flotaba como una especie de isla sobre el agua.
Pero, además de filósofo, ya en su época era reconocido como gran astrónomo al predecir un eclipse en el año 585 a.C. y como matemático o más precisamente geómetra, al comenzar a utilizar el pensamiento deductivo en geometría aportando a esta rama la enunciación de dos teoremas muy importantes que llevan su nombre, uno de los cuales surgió cuando descubrió cómo medir la altura de las pirámides valiéndose de la sombra que proyectan a cierta hora del día.
A continuación se desarrollan tres clases como Proyecto Temático para introducir a los alumnos en el mundo de la Proporcionalidad Geométrica y el gran aporte de Tales a través de su teorema.
Considerar que los contenidos previos necesarios para desarrollar el proyecto son:
- Razones.
- Proporciones. Propiedad fundamental y otras propiedades de las proporciones.
- Ecuaciones de primer y de segundo grado con una incógnita.
- Posiciones relativas de las rectas en el plano.
Clase 1
Se dibujan en el pizarrón dos segmentos AB y BD y se le pide a dos alumnos que pasen a medirlos: uno será de 24 cm y el otro de 1,5 cm.
Luego se les preguntará a los alumnos qué es una razón, para recordar el contenido, y a continuación se les preguntará cuál será la razón entre esos dos segmentos que nos permitirá saber cuántas veces entra el segmento de 1,5 cm en el de 24cm. Otro alumno pasará al pizarrón a escribir la razón: 24 cm/1,5 cm y el valor de la misma: 16.
Una vez visto esto se les da a los alumnos el concepto de razón entre dos segmentos: la razón entre dos segmentos es la razón o cociente entre sus medidas, ambas respecto de una misma unidad de medida.
Es importante aclararles que, al calcular la razón entre dos segmentos conocida la medida de cada uno de ellos, el resultado es siempre el mismo independientemente de la unidad de medida elegida, aunque debe ser siempre la misma para medir ambos segmentos. Para esto, se les puede proponer que lo verifiquen cambiando de unidad de medida: primero uno solo de los segmentos (por ejemplo el de 24 cm a 2,4 metros) y calculen la razón con el otro segmento sin cambiar, y luego que cambien también el otro segmento a la misma unidad que cambiaron el primero (en nuestro caso sería pasar el de 1,5 cm a 0,15 metros) y que calculen la razón entre los segmentos cambiados. Así verán que esta última razón también vale 16, pero que la otra no.
ACTIVIDADES PROPUESTAS
1) Escriban las dos razones que se pueden formar con los siguientes segmentos midiéndolos primero con una regla:
A B
C D
2) Escriban una razón entre un segmento de 20 dm y uno de 0,63 hm.
3) En este ejercicio tienes que calcular la razón de los segmentos AB y CD, en los siguientes casos:
| Medida de AB: | Medida de CD: | Razón AB/CD |
| a unidades | c unidades | a/c |
| 2 cm | 5 hm | |
| 3 m | 6 dm |
Clase 2
Se le pide a los alumnos que se agrupen de a dos o tres y a cada grupo se les entrega una hoja con el siguiente problema, que asemeja el trabajo que hizo Tales para calcular la altura de las pirámides:
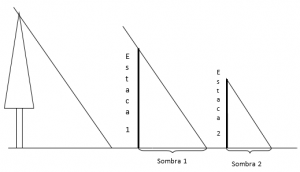
Un día soleado Martín salió a caminar por el parque con su amigo Juan. Mirando los rosales se dio cuenta de que las estacas que lo sostenían estaban colocadas en forma perfectamente verticales y, al observar esto, también se percató de que las estacas más altas proyectaban sombras más largas.
Juan, al verlo tan concentrado mirando los rosales, le preguntó en que estaba pensando. Cuando Martín le cuenta lo que pensaba, Juan le da otra información: que las sombras son proporcionales a las alturas, por eso con la ayuda de una estaca ellos podrían calcular la altura del pino que se encontraba al lado de los rosales, sin tener que medirlo. Entonces Juan propone a Martín ponerse a trabajar y medir las alturas y sombras de las estacas.
Midan ustedes también las alturas y sombras en el siguiente dibujo que representa la situación y completen la tabla, teniendo en cuenta que 1cm = 1m.
Tabla:
| Estaca 1 | Estaca 2 | |
| Altura | ||
| Sombra |
Una vez que completan la tabla se les pide que escriban la razón entre las alturas por un lado y la razón entre las sombras por el otro. Puede pasar un alumno a escribirlas al pizarrón. Luego deben sacar el valor de estas dos razones que darán lo mismo. A continuación se les preguntará si recuerdan qué es una proporción, y, según esto, se les preguntará si era cierto lo que Juan le había contado a Martín: que las sombras eran proporcionales a las alturas. Luego se les pedirá escribir la proporción entre las alturas y las sombras.
Para cerrar esto se les dará la definición de segmentos proporcionales: dos segmentos AB y CD son proporcionales a otros dos EF y GH si sus razones son congruentes, es decir, AB/CD=EF/GH . Luego los alumnos deberán señalar estos segmentos en el dibujo.
Se les dirá también que recuerden la propiedad fundamental de las proporciones, se le puede pedir a un alumno que la enuncie y a otro que pase a dar un ejemplo. Luego de esto, se les pedirá que calculen la altura del pino armando una proporción y brindándoles como dato la longitud de la sombra que proyecta.
ACTIVIDADES PROPUESTAS
1) Sean los segmentos:
a = 2 m, b = 3 m
c = 4 m y d = 6 m
Escribe todas las proporciones posibles entre ellos, y en cada caso den el valor de la razón de proporcionalidad.
2) Un número es igual a 275 veces otro número y la razón de estos dos números es 7/12. Hallar dichos números.
3) Los lados no paralelos de un trapezoide miden 10 y 15 cm, respectivamente. Una recta paralela a las bases divide al lado de 10 cm en la razón 1/4. Encontrar en qué razón queda dividido el segmento que mide 15 cm.
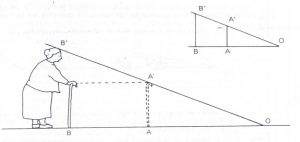
4) Es sabido que el sol incide con igual inclinación sobre los cuerpos en un determinado momento y lugar. Observando el esquema y usando la regla compara la altura de la abuela y del bastón con sus respectivas sombras y comprueba que son proporcionales. ¿Se podrá predecir la sombra producida por un árbol de 4,5 m de altura en el mismo momento y lugar? Calcúlenla.
Clase 3
Se les planteará a los alumnos la siguiente situación:
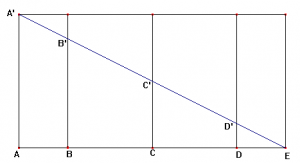
Habrá una lámina en el pizarrón con el siguiente dibujo, que los alumnos deberán copiar en sus carpetas:
Se les dirá que el dibujo representa un portón hecho por un herrero. Según este herrero, construyó este portón conservando una relación de proporcionalidad entre los segmentos ED’, D’C’, C’B’ Y B’A’ de la barra reforzadora (EA’) y la medida del ancho de cada lámina SD, DC, CB y BA que forman el portón. Se les pedirá entonces que encuentren la medida de las láminas que hay en los extremos.
Luego de un tiempo pasará un alumno a escribir lo que hizo en el pizarrón y si alguno planteó una proporción distinta también pasará al pizarrón y se verá en conjunto que son las mismas, por ejemplo, un alumno pudo haber tomado la proporción A’B’/AB=B’C’/BC y otro pudo haber tomadoA’B’/B’C’=AB/BC (los mismo pasa en el caso de que tomen las proporciones de los segmentos del otro lado del portón.
Una vez que obtuvieron las medidas se les pedirá que verifiquen las siguientes proporciones:
1) ED’/ED=EC’/EC 2) EA’/EB’=EA/EB 3) D’B’/DB=D’C’/DC
Luego se les dirá que verifiquen que, a su vez, las tres proporciones tienen la misma razón de proporcionalidad y se les pedirá que escriban en sus carpetas más proporciones entre los segmentos del portón.
También se trabajará con el grupo de segmentos AA’, BB’, CC’ Y DD’, preguntándolo a todo el grupo si también cumplen la relación de proporcionalidad como los otros segmentos, lo que tendrán que comprobar sacando la medida de cada uno de ellos. Luego podrán armar otras proporciones con estos segmentos.
Por último, se les preguntará a los alumnos cómo son las barras del portón entre sí (paralelas). Se les dirá luego que éstas paralelas están cortadas por dos transversales que determinan los segmentos proporcionales con los que estuvieron trabajando y se les preguntará cuáles son esas dos transversales, puede pasar un alumno a marcarlas con color en la lámina.
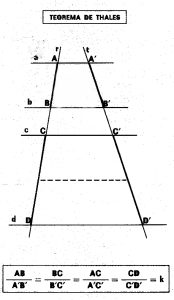
Así, después de todo este trabajo, los alumnos verán que estas rectas cortadas por dos transversales determinan segmentos proporcionales, por lo tanto se les dirá que esta propiedad es lo que se denomina Teorema de Tales y, a continuación, se les dará el enunciado, acompañado de una representación gráfica del mismo.
Teorema de Tales: Si tres o más rectas paralelas son cortadas por dos transversales, los segmentos determinados en una de ellas son proporcionales a los segmentos correspondientes determinados en la otra.
Se volverá luego a mirar el problema de la actividad anterior que debieron resolver sobre la altura de la abuela y su bastón y la longitud de sus respectivas sombras, que eran proporcionales, para que ellos vean que se cumple el Teorema de Tales, mirando principalmente la representación que tenían del problema y marcando en él las paralelas y transversales.
Hasta aquí la introducción al Teorema de Tales, luego habrá un sin fin de temas, actividades, aplicaciones y marcos matemáticos que se puedan abordar para la profundización del tema, dependiendo de contenidos previos y el año curricular en el que se encuentren nuestros alumnos.





Hola tendrías alguna clase virtual para plantearle a los estudiante. Aparte de ver videos.
MMm hola esta chica ya no escribe más en la revista. Lo siento