Geogebra es un software de Matemática que según la página oficial, se define como “la calculadora gráfica para Geometría, Álgebra, Cálculo, Estadística y 3D!”, y qué mejor instrumento para la enseñanza y aprendizaje de nuestros alumnos, que uno con el cual poder trabajar todos estos marcos de la Matemática de forma interactiva, con construcciones en manos de los chicos y que los motive desde un interés hoy más innato en los jóvenes: el uso de computadoras, tablets, celulares, etc., interés que hasta puede lograr motivar el uso de este programa fuera de la escuela.
Visto y considerando nuestra actualidad, me atrevo a decir que casi todos los profesores de Matemática conocemos este programa, pero para aquellos que no lo conocen o si alguno no se ha animado todavía a explorarlo, pueden descargarlo desde el sitio oficial: www.geogebra.org
Allí encontrarán los links de descarga para tablets, PC’s de escritorio y también hay una aplicación para celulares. Además, cuentan con la versión on-line, que permite utilizar Geogebra sin descargar el programa, pero necesariamente deben estar conectados a internet. También encontrarán en la página tutoriales para el usuario (http://www.geogebra.org/manual/es/Tutoriales) , que van desde la descarga e instalación del programa y el uso de las funciones más básicas, hasta algunos “trucos” que no se encuentran o se logran a simple vista. En la ventana principal de la página, también hay un apartado sobre propuestas y recursos para trabajar con el programa. En sí, la aplicación es de fácil ejecución, y cuánto uno más explora, descubre más funciones y combinación de funciones que parecieran nunca acabar.
Volviendo al aula, un tipo de actividad que quería traerles en esta nota, de especial interés para trabajar con nuestros alumnos, consiste en la construcción de figuras geométricas con la condición de que al moverlas, achicarlas o agrandarlas, es decir, al cambiar alguno de sus parámetros, conserven sus propiedades y sus dimensiones de forma proporcionada. En Geogebra existen los comandos para construir cualquier tipo de polígonos, regulares, rígidos, etc. Pero la idea, en el tipo de actividad que quiero plantear, es valerse solamente de puntos, segmentos y rectas, logrando construir una figura que no se “desarme”, poniendo en juego para esto, la dependencia y las propiedades de puntos y rectas, cuando uno realiza una construcción en Geogebra.
Supongamos la siguiente consigna: Sin utilizar el comando “polígono regular”, construir un cuadrado, de forma tal que al mover uno de sus puntos libres la figura continúe siendo un cuadrado.
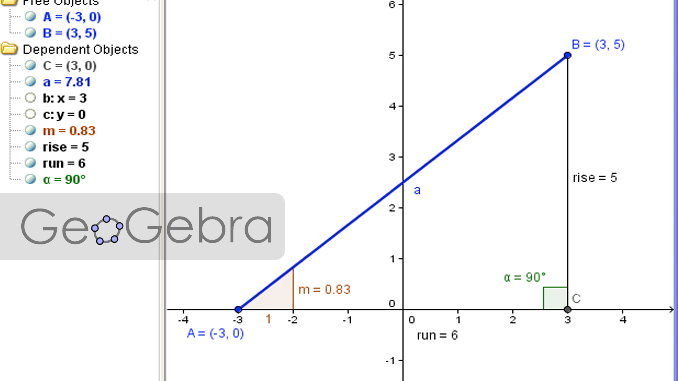
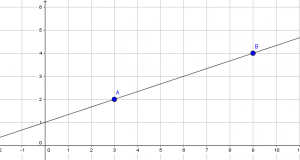
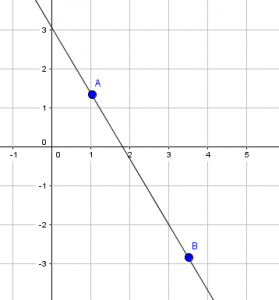
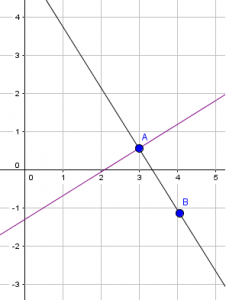
A saber: un objeto libre en Geogebra es aquel cuya posición o valor en el plano no depende de otro objeto. Hay también objetos dependientes, que son creados a partir de otros objetos y, por lo tanto, su valor o posición dependen directamente de dichos objetos que le dieron origen. Por ejemplo, si trazo una recta r en el plano, se marcarán dos puntos A y B. Tanto la recta como los dos puntos son libres, ya que es posible moverlos en el plano y cambiar su posición, como se ve en las siguientes imágenes:
Cabe aclarar que en las imágenes utilicé el plano coordenado y cuadriculado, para que los que desconocen este programa, logren una mejor visualización del desarrollo de esta nota.
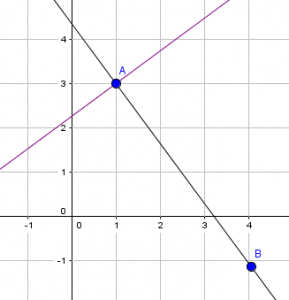
Ahora bien, si trazo una nueva recta f (violeta), perpendicular a la recta r, por uno de los dos puntos (supongamos que por el punto A), esta nueva recta no podrá moverse en el plano a no ser que mueva la recta r o alguno de los dos puntos. Por ejemplo, en las imágenes podemos observar cómo la recta f se mueve al trasladar el punto A.
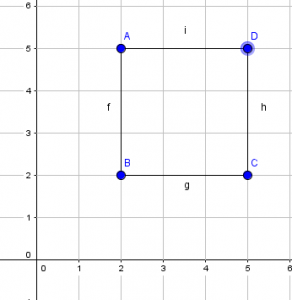
Volviendo a la consigna propuesta, podríamos pensar que en un principio los chicos dibujen el cuadrado utilizando cuatro puntos libres, uniéndolos con segmentos, valiéndose de una cuadrícula para que los lados tengan la misma longitud y sean perpendiculares. Pero, al mover uno de los puntos libres, la figura se deformaría, ya que los datos que se usaron fueron construidos independientes entre sí:
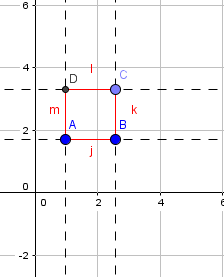
No estaría entonces cumpliendo con la consigna. Los alumnos deberán recurrir a otras herramientas para lograr la dependencia que necesariamente debe existir entre los objetos, y para esto, se les puede sugerir que piensen en las propiedades que cumplen los lados de un cuadrado, por ejemplo, que los lados consecutivos son perpendiculares y los opuestos son paralelos. Una dificultad para los chicos, que hay que tener en cuenta en este punto, es que Geogebra permite construir rectas paralelas o perpendiculares, pero no segmentos paralelos o perpendiculares. Para salvar este obstáculo hay que recordar a los alumnos que los segmentos están contenidos en las rectas, por lo tanto, al finalizar la construcción, se pueden ocultar las rectas o cambiarlas a un trazo punteado y construir sobre ellas los segmentos deseados, hasta eligiendo distintos colores (como se ve en las imágenes de abajo).
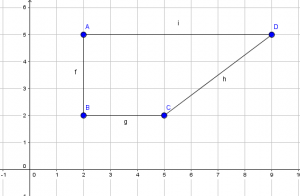
Retomando la construcción, tengan en cuenta que si los chicos sólo utilizan la perpendicularidad, nuevamente se encontrarán con que al finalizar la construcción, al mover uno de los puntos libres, la figura tomará la forma de un rectángulo, esto pueden probarlo haciendo ustedes mismos la construcción.
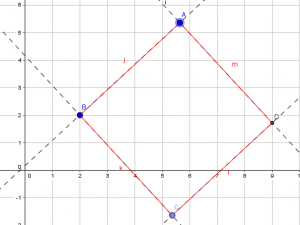
Ahora bien, si combinan rectas paralelas y perpendiculares de forma adecuada, podrán obtener la figura que cumpla con la consigna deseada. Por ejemplo, en las imágenes de abajo, primero construímos la recta j que pasa por A y B. Luego, la recta k que es perpendicular a j por el punto B, la recta l será paralela a j por el punto C y la recta m es perpendicular a l por el punto D. Los puntos C y D, son objetos dependientes, porque aparecen al construir las rectas paralelas y perpendiculares, por eso tienen otro color, es algo que el programa hace por defecto. Vemos en la sucesión de imágenes que, al mover los puntos libres A o B el cuadrado no se deforma y conserva todas sus propiedades.
Todas las construcciones de prueba y error que realicen los chicos sirven para ir aprendiendo sobre el programa y sobre la dependencia entre objetos. Sería importante que una vez que descubran una construcción que cumpla con la consigna, escriban el paso a paso, utilizando los nombres de rectas y puntos y los comandos que aplicaron.
Como última construcción se les puede pedir que realicen la misma sobre el plano sin cuadrícula ni ejes, tomando de forma aproximada la longitud de los lados, ya que una ventaja que tiene Geogebra es la Vista Algebraica, donde se pueden ver todas las coordenadas y medidas de los objetos construidos.
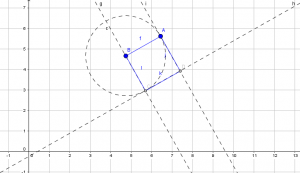
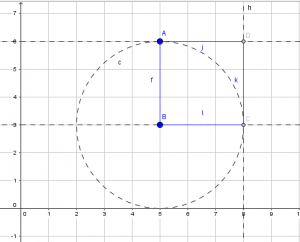
Además, se podría presentar a los alumnos un paso a paso para que realicen otro tipo de construcción de la misma figura, por ejemplo, podrían realizar una construcción valiéndose de los comandos “rectas perpendiculares”, “circunferencia (centro y punto)” y “recta tangente”. Les dejo un dibujo de la construcción para que intenten realizarla ustedes mismos. Observen cómo al mover cualquiera de los objetos libres, el cuadrado se conserva, ¿por qué? ¿Tiene que ver esto con el concepto de circunferencia? Les dejo estos interrogantes para ustedes y luego, si lo aplican en clase, para sus alumnos.




Sé el primero en comentar